Choosing a Tram Route: An Experience in Trading-Off Constraints

Ian Alexander, Scenario Plus Ltd

iany @ scenarioplus.org .uk

Abstract

Trading-off is a familiar element in requirements practice, but it generally assumes a set of independent requirements competing for resources. Choosing a tram route depends instead on trading-off competing pressures from stakeholders and other constraints, such as cost/benefit, buildability, safety, and disturbance to townscape, parks, wildlife, heritage, and housing, in a way that satisfies a public inquiry. There is no perfect way to do this, but several simple techniques and rules-of-thumb can be combined to do much better than seems to be usual. The approach adopted on this project consists of triage followed by evaluation. This splits the route into independently prioritisable partial routes. These are scored using hierarchically weighted criteria.

1           Introduction

Requirements textbooks [1, 2, 3] implicitly assume that trading-off (usually in the shape of prioritisation) is needed because a resource such as money or time is limited. However, some practical problems still present difficulties even if ample money and time are available. Choosing the route of an urban light railway (tram, Figure 1) depends on trading-off competing constraints such as cost/benefit, buildability, and disturbance to townscape, parks, wildlife, heritage, and housing.

Figure 1: Tramway on a Suburban Street

Whereas textbooks [1, 2, 3, 4, 5] tend to assume that requirements are mainly functional and for a wholly new “green field” system, and that stakeholders can, within reason, get whatever they want if enough money is provided, urban railways are practically guaranteed to go through somebody’s backyard. Functions are few (basically, carry N passengers per hour, with journey time J). The development is extremely “brown field” with many interfaces and existing assets to constrain every choice. Constraints are experienced as competing stakeholder pressures. Contrary to RE dogma, success cannot be assured just by stating clearly what you want.

There may be few or no written requirements, as the components that would need to be specified in detail – rolling stock and signalling – are generally procured as a whole from a manufacturer’s product catalogue, while local decisions such as the design of crossings are covered by a large body of existing standards,  legislation, and industry best practice [e.g. 6, 7].

In contrast to the lack of hard-and-fast requirements, there are many constraints. Gause & Weinberg [4], as concisely explained by Sutcliffe [5], suggest relaxing constraints as one way to resolve requirements conflicts; most of their other suggestions relate to dealing with stakeholders personally to reduce tension – not necessarily possible when the public is involved.

Some tram routing constraints can be relaxed, and some cannot. This is because many stakeholder groups are involved [8], each typically interested in protecting a certain kind of asset (e.g. parks, historic buildings, wildlife, a business), and some are very powerful.

The general process in the UK for conducting transport projects that will impinge on the public is to obtain an Order under the Transport and Works Act (TWA) [9]. Similar processes exist in other countries. The TWA process culminates in a public inquiry and a decision by the Secretary of State for Transport, a government minister. Anyone can object at the public inquiry, potentially causing serious upset – delay or cancellation – to the project at a late stage.

Therefore it is critical for the project to identify stakeholders, to discover their points of view, and to design the transport scheme so as to cause minimal difficulty. In the case of institutional stakeholders, direct negotiation (in advance of the inquiry) is often possible. In the case of the public, however, where many conflicting opinions may exist, consultation (combining public meetings, leaflets, and written submissions) is the only option, and it is quite a limited mechanism.  Full agreement is hard to obtain.

A key element in the design of a transport scheme is often the choice of route. Alternative route options may affect different stakeholders, and each part of the route may arouse passionate opposition from one or another group. In effect, therefore, the different stakeholders apply competing pressures to the project. 

There is no perfect way to handle competing pressures, but several simple techniques and rules-of-thumb can be combined to do much better than seems to be usual. There is a clear need for a fair, repeatable route selection approach, defensible at public inquiry. This paper describes the approach taken on one transport project. It is structured as follows:

Section 2 states the problem.

Section 3 describes the approach taken on the project.

Section 4 discusses some possible conclusions.

2           The Problem

The experience described here relates to a specific urban light railway, which is still in the planning phase and is therefore confidential. However the issues encountered, and the techniques developed to deal with them can readily be explained with a fictitious example chosen to bring out the key aspects of the real route selection problem.

The City Tram is to relieve traffic congestion by providing a reduced journey time from A to B. With closely-spaced stops at places such as C, D, E, F, G, H, and an interchange with the railway at B, it should encourage economic growth in the City.  A stop at D could encourage further expansion of the tram to the north. However there are obstacles as follows (Figure 2).

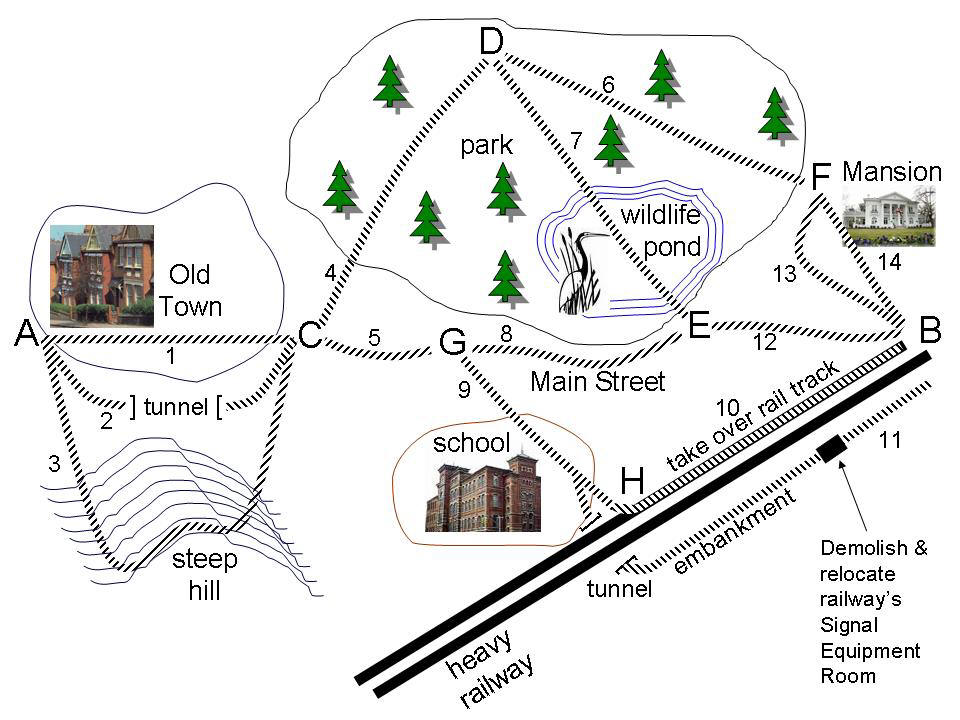
Figure 2: Candidate Route Segments for City Tram

Between A and C there is an old town with an attractive townscape to the north. To the south is a steep hill which could cause the tram operational difficulties in wet or icy weather. A central route is imaginable but would require a costly tunnel through the hill.

Between C and E/F is the town park with scenic views, mature trees and a wildlife pond. Near F is the Mansion, a Grade I historic building. Exiting the park at E would avoid the mansion but would harm the wildlife pond. A partial alternative is to route the tram in a semicircular arc between F and B so as to avoid the street immediately in front of the Mansion.

The park could be avoided by a route through G south of the park, but the route from G to E is along busy Main Street, threatening to worsen the traffic congestion rather than alleviating it.

An alternative to Main Street is the route southeast from G to the heavy railway at H, but unfortunately this crosses the School’s playground: this could cause strong local opposition to the tram. From H to B the tram could run on one of the existing railway tracks, if the railway company can be persuaded to give it up, or it could run on top of the embankment on the south of the railway line. However the embankment route would demand a tunnel to cross the railway, and the demolition and re-siting of the railway’s Signal Equipment Room, which the railway company opposes. The tunnel would raise buildability issues, as access to the railway is limited, and closures would have to be planned for nights and weekends.

The problem, therefore, is to choose a route  acceptable to public inquiry, by trading-off these constraints. Few of them are hard-and-fast requirements, but trading demands sensitive stakeholder management and thorough stakeholder identification [8]. Success at public inquiry demands a convincing case: in RE terms, traceability and justification are critical.

3           Approach Taken on the Project

Transport planners began with a few high-level goals, such as to improve accessibility, prosperity, fairness and quality of city life by improving the transport network. These led them to evaluate candidate routes for their predicted cost and benefit. Direct benefits were measured e.g. by journey time reduction. Costs were estimated as usual by making an outline design and identifying cost elements along the route, e.g. bridges and crossings. Indirect benefits are problematic, but were evaluated by e.g. estimating additional numbers of passengers visiting shops, possible rises in house prices, and so on.

3.1           Triage

Such preliminary considerations permitted the early elimination of many candidate routes. In contrast to the view of requirements triage presented in Davis’ stimulating book [10], it seems useful to take triage as something different from prioritisation and indeed option selection in general. Davis defines triage as

“determining which requirements should be satisfied when analyzed within the context of available development resources, time to market, revenue goals, and return on investment.” (page 6)

A transport project, on the other hand, trades off a set of constraints: it makes no sense to satisfy one such constraint (e.g. avoid busy roads) perfectly at the expense of another (e.g. avoid parks). However, going back to the original medical meaning of triage works well in this context. The triage nurse examines the casualties and splits them into 3 categories:

1)       those that will die even if treated (at the expense of other casualties);

2)       those that will live even if not treated;

3)       those that will benefit from treatment.

Translating this into transport planning terms, we get 3 outcomes for a candidate route:

1)       routes that are plainly not acceptable;

2)       routes that are plainly acceptable;

3)       routes that need further evaluation.

Removing plainly unacceptable (type 1) candidate routes in a triage step early in planning is valuable, as it avoids wasting effort. (It is however still necessary to document why a candidate was rejected, to show that the process was fair.) The potential waste is large, both because evaluating routes (basically by designing them) is costly, and because there is often a combinatorial explosion of routes through a network of possible route segments to consider (see below). Reducing the number of route segments efficiently prunes the search space. On this project, transport planners triaged out numerous candidate routes and route segments before evaluation.

It is a lucky transport scheme that finds an entire non-contentious (type 2) route, but some route segments may be so, eg where a route can traverse a disused stretch of railway or industrial land.

The remaining routes or route segments need to be evaluated further. In this approach, therefore, triage is a preliminary to detailed evaluation.

3.2           Divide and Conquer at Centre Nodes

There are 18 combinations of route segments for the City Tram on Figure 2. Longer routes experience an explosion in the number of combinations (roughly with the square of the length and complexity of the route). This creates a heavy potential workload for the project, evaluating every route against every criterion.

One useful technique is to examine the network of route segments for what can be called “Centre Nodes” like C: all possible routes from A to B pass through C. Therefore, the task of finding the best route is reduced to finding the best partial route from A to C, and the best from C to B. In this case, there are 3 candidates between A and C, and 6 between C and B, for a total of 9 evaluations instead of the original 18, ie this halves the evaluation workload for no change in the quality of the result. On complex routes, the saving is greater.

When no Centre Node exists – for example, if there was an additional route segment between A and D, avoiding C – then it is harder to avoid evaluating all possible routes, and indeed that may be the only defensible procedure. Sometimes it may be reasonable to argue that, say, the segment from A to D is clearly less beneficial than the other routes, or clearly involves certain awkward problems of cost, buildability, etc. In that case the problem can be reduced by treating C as a Centre Node. But such reasoning is always vulnerable to cross-questioning at public inquiry.

3.3           Traditional Scoring

The usual approach taken on route projects is to score each route (segment) on each criterion. The score may then be weighted. The obvious problem is that the measures on the criteria will be different – adding apples and oranges.

Table 1 is a fragment from [11], part of the UK government’s NATA guidance on transport appraisal. Like many business process frameworks, NATA contains much common sense distilled from experience. But there are several problems with NATA-style evaluation.

Firstly, the assessment measures such as scores for impact on Biodiversity, tonnes of CO₂ for Greenhouse Gases, and the cash cost of Accidents are on different dimensions and cannot be combined directly.

One approach is to try to convert everything to money. Unfortunately this is hard to do for criteria such as Ambience. Even for criteria such as Physical Fitness which have money implications – a healthier population costs less in medical care, for instance – there are benefits such as improved feelings of well-being that cannot be quantified.

Table 1: NATA Appraisal Summary Table (fragment)

An alternative is to argue that, say, Accidents are more important than Ambience, and should be given a relative weight of 3. This raises a further problem, which is that assigning a long list of weights is difficult and subjective. There is a strong temptation to adjust the weights to make the desired route win – the opposite of the intended result of the process. A more defensible procedure is described below in section 3.4.

 Secondly, there is a serious issue of fairness at the “Objective” (parent criterion) level. Environment contains 10 criteria, Safety only 2. If weights are not used (as has been observed) or if the weights are weak (eg ranging only from x1 to x3, as has also been observed on a project) then “Objectives” containing many “Sub-Objectives” (child criteria) will have unfairly large importance. Environment should not be 5 times as important as Safety in evaluating a route.

Thirdly, projects vary widely. No fixed approach such as that of Table 1 can work well in every case. Also, the list of criteria is unbalanced: strong on Economic factors, but ignoring important factors such as Buildability. This covers all issues of construction, such as how hard it is to reach each site, or disturbance to neighbours and existing assets (eg gas mains) during building. NATA handles these elsewhere, but without taking them into account for route evaluation. The project therefore added a new “Objective” for Buildability, as well as some Sub-Objectives to the existing categories.

3.4           Hierarchical Weighting

Since Tram projects are expected to comply with NATA, the project team considered how to make the approach more defensible. [12] describes a hierarchical weighting approach used for tender evaluation, ie the problem of fairly comparing competing proposals for a project. That approach involves several complex safeguards such as using teams of assessors and averaging scores for each candidate on each criterion. Ignoring these refinements, the basic concept is a triage element – FAIL is a possible score on “critical” criteria, with hierarchical assignment of weights.

Hierarchical weighting was applied as follows. The “Objectives” (parent criteria) were listed on a spreadsheet, with their “Sub-Objectives” grouped beneath them. The task of combining the scores on all the Sub-Objectives is reduced to weighting the Objectives against each other, to a normalised total of 100 (%), and then weighting the Sub-Objectives within each group against each other (locally), again to a normalised total of 100. This procedure can, if need be, be applied at any number of levels of hierarchy.  Its advantage is that it is a relatively easy task to rank a small set of criteria against each other.

 Table 2: Weighting the Parent “Objective” Criteria

On the tram project, the team assigned “Objective” weights as in Table 2. Safety and the Environment can be seen to have been judged the major criteria.

Table 3: Scoresheet (fragment)

Table 3 shows a fragment of a score-sheet. The parent (“Objective”) weights are multiplied by the individual child weights and scores shown in Table 3 for all the “Sub-Objective” criteria, and summed to yield subtotals.

A column is provided for each route segment to be compared, in this case the three segments between A and C on the map. The six partial routes between C and B are scored and weighted in the same way.

Each route segment was scored on each criterion by a single expert, and the weighted scores summed to give a single total score for each route segment. The bottom row of Table 3 shows the subtotals for the Environment Objective: the overall totals are not shown. In this case, the route via the tunnel scores the highest. 

3.5           Sensitivity Analysis

The obvious threat to the validity of any weighting scheme is to wonder whether the assigned weights are justified. There is no perfect counter to this threat. What can be done, however, is to analyse the sensitivity of the result to the assigned weights. If the result varies little over a wide range of weightings, it can be argued that the outcome is probably the best that can be achieved.

To conduct the sensitivity analysis, copies of the original spreadsheet were modified systematically. Each “Objective” weight was varied by a chosen large amount, and all the other “Objective” weights were varied in the other direction by a small amount to compensate (ie the total had to remain at 100%). For example, on one sheet the Safety weight was decreased by 10%, down to 15%, while Environment and all the other weights were increased by 2%.

Note that a change in weighting of 10% is a very large swing: for example, in the case of Buildability, which began at 10%, adding 10% means doubling its weighting, while subtracting 10% means reducing its influence to zero.

Table 4: Sensitivity Analysis (fragment of one sheet)

Table 4 shows a fragment (of the -10% sheet) of the results of the sensitivity analysis for one set of alternative route segments on the tram project (comparable to the set of route segments between A and B in the fictitious example). There are (not shown) matching results for ‑5%, +5%, and +10%. In addition, where the winner changed at +/-5%, a +/-2.5% sheet was evaluated. The top part of Table 4 shows how the weights were varied to explore sensitivity: each column represents one copy of the original scoring spreadsheet, with weights varied as shown.

The bottom part shows the results. The original winning route segment is shown as “B”. B still wins when Environment, Accessibility, or Buildability are varied by -10%. Economy and Integration  gave a different winner, “A”, at -5%, and Safety (highlighted) made A the winner at -10%.

Table 5 summarises all the sensitivity analysis results for this set of six competing route segments. Each cell of Table 4 shows the winning route with the indicated combination of changes, e.g. varying Safety’s weight by ‑10% made “A” the winner. (Table 4’s “Winner” row for -10% forms the first data row of Table 5.)

Table 5: Sensitivity Analysis Summary

These results were reassuring to the project, as they show that over a wide range of weighting schemes, either the original winner remains the winner, or the original runner-up wins.

Further, the original winner became the runner-up in all but 4 cases out of 27 evaluated in the sensitivity analysis. If the analysis had shown that many different options could win or become runner-up (unpredictably) as different weights were chosen, this would have indicated that the weighting scheme was unreliable.

As it is, the results give an assurance that either the original winner or the runner-up constitute the best  options for this part of the route, enabling human judgement to be applied efficiently to compare the merits of these two route segments.

4           Discussion

Objectivity

It is not ideal for one individual to attempt to score candidate routes on all criteria. It is easier to justify having experts in the different dimensions – wildlife impact, effect on road traffic, visual impact, etc – score the routes on the criteria they know about. Averaging the scores of several experts on each criterion may be better.

Quantifying the Unquantifiable

Scores on individual criteria are themselves hard to quantify. It is arguably more comfortable for experts to provide relative rankings than numeric scores. Ranking is easier to do, and one can have good confidence in a route’s ranking on a criterion, especially if different experts arrive at a similar result.  

Rankings provided by experts can be analysed with non-parametric statistics such as Spearman’s rank correlation coefficient or Kendall’s tau [13]. These may reveal correlations between some criteria, in which case those criteria can be grouped and evaluated together.

Unfortunately, these approaches do not reduce the problem to just one dimension, ie ranking the routes from worst to best by merging all criteria.

Perhaps project engineers should only evaluate, analyse rankings and select up to a point, leaving a small number of key choices up to other stakeholders. This was the position advocated by the consultant Sam Storey [14]. Effectively, the engineering part of evaluation would lead to statements like

“If you prefer parkscape to townscape, you’ll prefer route X to route Y, and vice versa”.

Public consultation does sometimes proceed with a small choice of alternative routes and an invitation to vote: a large number of choices would only cause confusion. However, a project must at some point come down to a single preferred route. Deferring the choice is costly, as it means developing detailed plans for more than one route.

Triage: This year… Never

Route triage and evaluation are somewhat different from the usual “this year, next year, sometime, never” prioritisation of features useful for product release planning. While the “this year” and “never” categories are applicable for route triage, the typical timing aspects of release planning are less so, as it is costly to modify a route once built. In contrast, features can be added relatively easily on other types of project, such as (in increasing order of difficulty) office software, embedded software, consumer electronics, or complex products (aircraft, warships). The tram case most resembles large civil engineering projects, eg a football stadium, in the need to get the requirements right first time.

It is true that on a larger scale (say, a city-wide programme of many individual route projects) it makes sense to plan successive stages as extensions to routes, probably over a time-scale of decades. However engineers on a given route project do not see all that.

Sensitivity Analysis Formalises Common Sense

Sensitivity analysis only demonstrates that the effect of a particular set of scores on a particular set of candidate routes is or is not relatively insensitive to changes in weighting scheme. Each project following this method must conduct its own sensitivity analysis for each comparison of routes. There is no guarantee that a good result will be obtained every time (a similar situation to the use of PCA, and for a similar reason). Common sense and engineering experience agree that selection is in general a hard problem: sometimes the results will be relatively stable, and sometimes they will be vulnerable to the slightest change in scores, criteria, or weights. Sensitivity analysis using the method illustrated formalises this intuition.

As a rule-of-thumb, if varying the weights by +/-5% does not change the winner, the results may be considered safe; the same at +/-10% would be very stable. If varying the weights by +/-5% either preserves the original winner or makes the runner-up win, as in the experience here, the results can be considered usable.

Hierarchical Weighting is Fairer

There is an inevitable “comparing apples and oranges” quality to route selection on multiple criteria. The whole process of collapsing multiple dimensions to a single score, by whatever weighting approach, is at best a rough-and-ready way of being fair.

A simple hierarchical weighting approach does not completely avoid the charge of being somewhat rough-and-ready. However, it is certainly fairer than both a naïve unweighted scheme and a naïvely weighted (non-hierarchical) scheme. Both of those remain in common use in route selection. Table 6 summarises the arguments.

Table 6: Weighting Approaches Compared

Automation by Shortest Path Algorithm

It would be possible to apply a Shortest Path algorithm to compare weighted scores on all route segments. That would demand scoring every segment in a network using the same weights. The project in fact only scored certain groups of route segments (between Centre and end nodes) in full detail, as triage was sufficient on some parts of the route. Automated Shortest Path scoring also remains vulnerable to challenge on grounds of unfairness of weighting, so other approaches such as sensitivity analysis or agreement by experts remain necessary.

A Stepwise Approach

In conclusion, a stepwise approach to route selection seems easier to justify, and to defend at public inquiry, than the traditional scoring approach. The steps adopted on the tram project were:

Triage:

1)       discard the unworkable routes

Evaluation:

2)       Identify any Centre Nodes to split the route into separately prioritisable partial routes

3)       Identify evaluation criteria (in groups)

4)       Assign normalised weights to each group

5)       Assign normalised weights within each group

6)       Score each partial route on each criterion (and calculate the sum of the weighted scores)

7)       Validate the outcome with Sensitivity Analysis.

All the evaluation data are recorded to support the choice of a preferred option at public inquiry, i.e. the whole process corresponds to a justification or legal argument for the choice.

The route selection problem is rather different from trading-off competing functional requirements for a software product. Indeed, it could be argued that on a transport scheme, trading-off constraints is the major requirements engineering task.

5           References

[1] I. F. Alexander & R. Stevens, Writing Better Requirements, Addison-Wesley, 2002.

[2] S. Robertson & J. Robertson, Mastering the Requirements Process, Addison-Wesley, 1999.

[3] I. Sommerville & P. Sawyer, Requirements Engineering, A good practice guide, Wiley, 1997.

[4] D. C. Gause & G. M. Weinberg, Exploring Requirements, Quality Before Design, Dorset House, 1989.

[5] A. Sutcliffe, User-Centred Requirements Engineering, Theory and Practice, Springer, 2002.

[6] Railways and Other Guided Transport Systems (Safety) Regulations 2006. (http://www.rail-reg.gov.uk/server/show/ConWebDoc.7964)

[7] HMRI Railway Safety Principles and Guidance, 1996 (http://www.rail-reg.gov.uk/server/show/nav.1096)

[8] I. F. Alexander, A Taxonomy of Stakeholders, Human Roles in System Development, International Journal of Technology and Human Interaction, Vol 1, No. 1, 23-59, January – March 2005.

[9] The Transport and Works Act, 1992. (http://www.opsi.gov.uk/acts/acts1992/Ukpga_19920042_en_1.htm)

[10] A. M. Davis, Just Enough Requirements Management, Dorset House 2005.

[11] Transport Analysis Guidance, Appraisal TAG Unit 3.2, February 2004. (http://www.webtag.org.uk/webdocuments/3_Expert/2_Appraisal/index.htm)

[12] K. Jackson, Tender Assessment Solution, FINSE, October 2000. (http://www.finse.org/2000Autumn/presentations/Tender_Assessment_Solution.pdf)

[13] C. Dytham, Choosing and Using Statistics, Blackwell, 2003.

[14] S. Storey, The Selection Problem, and Non-Parametric Statistics. Unpublished manuscript, Logica, 1986